100 Questions on Mathematics Optional for UPSC Civil Services

Introduction

Mathematics Optional in the UPSC Civil Services Examination is one of the most rewarding yet challenging choices. The subject requires logical thinking, clarity of concepts, and strong problem-solving skills. To help aspirants in their preparation, here are 100 carefully framed questions divided into chapters as per the UPSC Mathematics syllabus.

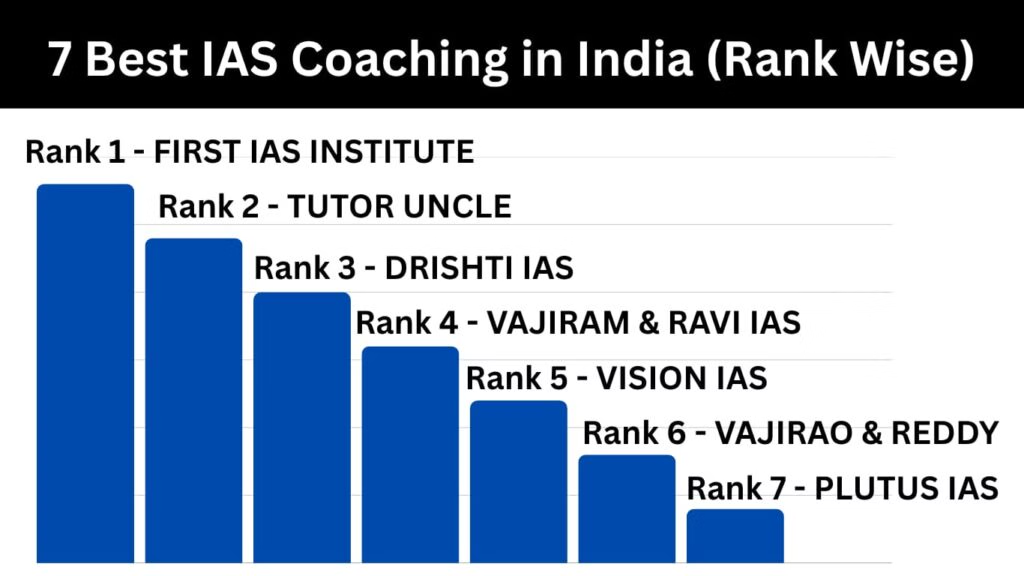
For UPSC Coaching , Join FIRST IAS INSTITUTE (India’s Top IAS Coaching)

Chapter 1: Linear Algebra

1. Define vector space with examples.
2. What are linearly independent and dependent vectors?
3. State and prove Rank-Nullity theorem.
4. Find the rank of a given matrix using elementary transformations.
5. Explain Eigenvalues and Eigenvectors with examples.
6. Solve a system of linear equations using matrix method.
7. What are orthogonal and unitary matrices?
8. Discuss Cayley-Hamilton theorem and its applications.
9. Find the characteristic polynomial of a given square matrix.
10. Define diagonalization of a matrix with conditions.

Chapter 2: Calculus

11. Differentiate between continuity and differentiability.
12. State and prove Rolle’s Theorem.
13. Explain Mean Value Theorem with an example.
14. Expand a function using Taylor’s theorem.
15. Discuss maxima and minima of functions of two variables.
16. Find the radius of curvature of a curve at a point.
17. Evaluate a double integral over a region.
18. Convert a double integral into polar coordinates.
19. State and prove Green’s theorem.
20. Solve problems based on Stokes’ theorem.

3: Analytical Geometry

21. Find the equation of a plane passing through three points.
22. Derive the equation of a line in space in symmetric form.
23. Discuss condition for two lines in space to be coplanar.
24. Write the equation of a sphere with given center and radius.
25. Find the intersection of a line with a sphere.
26. Derive the equation of a cone with vertex at the origin.
27. Define paraboloid and find its equation.
28. Find the equation of an ellipsoid with given axes.
29. Derive the condition for tangency of a plane to a sphere.
30. Find the equation of the director sphere of a given sphere.

Chapter 4: Ordinary Differential Equations

31. Solve first order linear differential equations.
32. State and explain existence and uniqueness theorem.
33. Solve Bernoulli’s differential equation.
34. Explain method of variation of parameters.
35. Find particular integral of a second-order linear equation.
36. Solve Cauchy-Euler differential equation.
37. Solve simultaneous linear differential equations.
38. Define exact differential equations and solve examples.
39. Explain orthogonal trajectories with examples.
40. Solve second-order linear equations with constant coefficients.

Chapter 5: Dynamics and Statics

41. Derive equations of motion under uniform acceleration.
42. State Newton’s laws of motion with applications.
43. Discuss motion of a particle in a resisting medium.
44. Solve problems on projectile motion.
45. Derive expressions for work, power, and energy.
46. Discuss simple harmonic motion.
47. Explain equilibrium of coplanar forces.
48. Solve problems based on friction.
49. Derive conditions for equilibrium of a particle on a rough inclined plane.
50. State and prove Lami’s theorem.

6: Vector Analysis

51. Define gradient of a scalar function with example.
52. Explain divergence of a vector field.
53. Derive curl of a vector field.
54. State and prove Gauss divergence theorem.
55. Derive vector identities involving gradient, divergence, and curl.
56. Solve problems based on Stokes’ theorem.
57. Find potential function for a given vector field.
58. Discuss irrotational and solenoidal vector fields.
59. Define Laplacian operator and its applications.
60. Solve vector integration problems.

Chapter 7: Real Analysis

61. Define limit of a sequence with example.
62. Prove convergence of a monotonic sequence.
63. Discuss Cauchy’s criterion for convergence.
64. Define series of real numbers and convergence tests.
65. State and prove ratio test for series convergence.
66. Explain absolute and conditional convergence.
67. Expand functions using Fourier series.
68. Discuss uniform convergence of sequences and series.
69. Define Riemann integration with example.
70. Prove that a continuous function on [a, b] is integrable.

Chapter 8: Complex Analysis

71. Define analytic functions with examples.
72. Prove Cauchy-Riemann equations.
73. Discuss harmonic functions and their properties.
74. State and prove Cauchy’s integral theorem.
75. Derive Cauchy’s integral formula.
76. Define singularities and types with examples.
77. Expand a function into Laurent series.
78. State and apply residue theorem.
79. Evaluate improper integrals using residue theorem.
80. Solve problems based on conformal mapping.

9: Linear Programming

81. Define linear programming problem with example.
82. Explain graphical method of solving LPP.
83. Solve LPP using simplex method.
84. Discuss Big M method with example.
85. Explain two-phase simplex method.
86. Define duality in linear programming.
87. Prove fundamental theorem of duality.
88. Solve transportation problem using Vogel’s approximation method.
89. Discuss assignment problem with Hungarian method.
90. Solve integer programming problems.

Chapter 10: Mechanics and Fluid Dynamics

91. Derive equations for motion of a rigid body.
92. Discuss D’Alembert’s principle.
93. Derive moment of inertia of a rigid body.
94. State and explain principle of virtual work.
95. Discuss motion of a particle in a central force field.
96. Derive Euler’s equations of motion.
97. Explain Bernoulli’s theorem in fluid dynamics.
98. Derive equation of continuity for incompressible fluid.
99. Discuss Navier-Stokes equations.
100. Solve problems based on streamlines and potential flow.

Conclusion

These 100 questions on Mathematics Optional for UPSC Civil Services are designed to cover every chapter of the syllabus comprehensively. Aspirants should practice solving them regularly to build accuracy, speed, and conceptual clarity. With consistent preparation and analytical practice, Mathematics can become a high-scoring optional subject in the UPSC examination.

Also Visit – Best IAS Coaching in India

For Answer Writing Techniques – Join FIRST IAS INSTITUTE